Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Xin chào các bạn yêu quý của Loser1! Năm mới 2025 đã đến, và hôm nay chúng ta sẽ bắt đầu năm mới với một bài toán thú vị về đồ thị! Let’s make our first problem of 2025 count! 🎉
Table Of Contents
684. Redundant Connection
MediumTrong bài toán này, một cây là một đồ thị vô hướng được kết nối và không có chu trình.
Bạn được cung cấp một đồ thị bắt đầu như một cây với n nút được đánh nhãn từ 1 đến n, với một cạnh bổ sung được thêm vào. Cạnh được thêm vào có hai đỉnh khác nhau được chọn từ 1 đến n, và không phải là cạnh đã tồn tại. Đồ thị được biểu diễn dưới dạng một mảng edges có độ dài n trong đó edges[i] = [ai, bi] chỉ ra rằng có một cạnh giữa các nút ai và bi trong đồ thị.
Trả về một cạnh có thể được loại bỏ để đồ thị kết quả là một cây của n nút. Nếu có nhiều câu trả lời, hãy trả về câu trả lời xuất hiện cuối cùng trong đầu vào.
Example 1:
Input: edges = [[1,2],[1,3],[2,3]] Output: [2,3] Explanation: Cạnh [2,3] là cạnh thừa có thể được loại bỏ để đồ thị trở thành một cây.
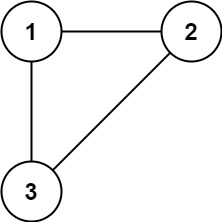
Example 2:
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]] Output: [1,4] Explanation: Cạnh [1,4] là cạnh thừa có thể được loại bỏ để đồ thị trở thành một cây.
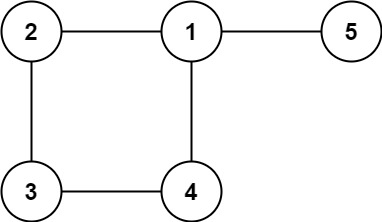
Constraints:
n == edges.length3 <= n <= 1000edges[i].length == 21 <= ai < bi <= edges.lengthai != bi- Không có cạnh nào bị lặp lại.
- Đồ thị đã cho được kết nối.
First Thoughts & Intuition 🧠
Khi nhìn vào bài này, mình liên tưởng đến việc trang trí cây thông năm mới:
1. Tree vs Graph 🎄
Tree hợp lệ: Graph có chu trình:
1 1
/ \ / \
2 3 vs 2---3
Giống như khi trang trí:
- Đèn phải được kết nối (connected)
- Không được tạo vòng (no cycles)2. Phân tích Pattern 🎯
Ví dụ 1: Ví dụ 2:
1---2 1---2
\ / \ \
3 4---3
|
53. Key Insights 💡
Observation 1: Tree Properties
- n nodes
- n-1 edges
- no cycles
Observation 2: Redundant Edge
- Edge thứ n tạo cycle
- Cần tìm edge cuối cùng tạo cycleSuper Detailed Approach 🎨
1. Union-Find Implementation 🚀
C++
class UnionFind {
vector<int> parent, rank;
public:
UnionFind(int n) : parent(n+1), rank(n+1, 0) {
// Initialize mỗi node là một set riêng
for(int i = 0; i <= n; i++)
parent[i] = i;
}
int find(int x) {
// Path compression
if(parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
bool unite(int x, int y) {
int px = find(x), py = find(y);
if(px == py) return false; // Đã cùng set -> tạo cycle
// Union by rank
if(rank[px] < rank[py]) swap(px, py);
parent[py] = px;
if(rank[px] == rank[py]) rank[px]++;
return true;
}
};2. Main Solution 🎯
C++
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
UnionFind uf(n);
for(auto& edge : edges) {
if(!uf.unite(edge[0], edge[1])) {
return edge; // Edge này tạo cycle!
}
}
return {}; // Không tìm thấy (impossible)
}
};Example Walkthrough 🎮
Input: edges = [[1,2],[1,3],[2,3]]
Step 1: Initial State
1 2 3 (Mỗi node là một set)
↓ ↓ ↓
1 2 3
Step 2: Add edge [1,2]
1---2 3 (Unite 1 và 2)
↓ ↓
2 3
Step 3: Add edge [1,3]
1---2 (Unite 1 và 3)
\ ↓
3←┘
Step 4: Add edge [2,3]
1---2 (Try unite 2 và 3)
\ / CYCLE DETECTED! 🚨
3 Return [2,3]Visual Explanation 🎨
Detecting Cycles with Union-Find:
Before: After:
1 2 3 1---2
\ |
\ |
\ |
3
CYCLE!Complexity Analysis 📊
Time: O(N * α(N))
└── N: số lượng edges
└── α(N): Inverse Ackermann function
└── Gần như O(N) trong thực tế
Space: O(N)
└── Parent array
└── Rank arrayTips & Tricks 💡
- Union-Find Optimization:
- Path Compression trong find()
- Union by Rank
→ Gần như O(1) cho mỗi operation!- Edge Cases:
Minimum case: Maximum case:
1---2 1---2---3
\ / | | |
3 5---4---6- Implementation Tips:
- Use 1-based indexing (nodes từ 1 đến n)
- Return cạnh cuối cùng tạo cycle
- Check connection trước khi uniteChúc mừng năm mới 2025! Hy vọng năm mới sẽ mang đến nhiều thuận lợi trong hành trình học tập của các bạn! 🎊
P/S: Follow mình tại Learning AI with Loser để cập nhật các bài giải Leetcode hàng ngày nhé! 💻✨
CODE EDITOR
#leetcode #leetcodedaily #algorithms #programming #learningwithlosers #newyear2025
