Xin chào mọi người! Mình là Loser1 từ Learning AI with Loser. Hôm nay chúng ta sẽ đi vào một bài toán thú vị về game strategy – nơi hai robot đối đầu nhau trong một cuộc đua điểm số! Let’s dive in! 🎮

2017. Grid Game

Medium

Solved

You are given a 0-indexed 2D array grid of size 2 x n, where grid[r][c] represents the number of points at position (r, c) on the matrix. Two robots are playing a game on this matrix.

Both robots initially start at (0, 0) and want to reach (1, n-1). Each robot may only move to the right ((r, c) to (r, c + 1)) or down ((r, c) to (r + 1, c)).

At the start of the game, the first robot moves from (0, 0) to (1, n-1), collecting all the points from the cells on its path. For all cells (r, c) traversed on the path, grid[r][c] is set to 0. Then, the second robot moves from (0, 0) to (1, n-1), collecting the points on its path. Note that their paths may intersect with one another.

The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot.

Example 1:

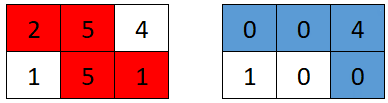
Input: grid = [[2,5,4],[1,5,1]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
       

Example 2:

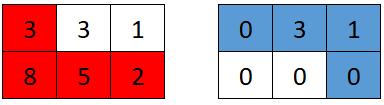
Input: grid = [[3,3,1],[8,5,2]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
       

Example 3:

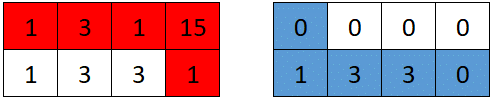
Input: grid = [[1,3,1,15],[1,3,3,1]]
Output: 7
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
       

Constraints:

• grid.length == 2
• n == grid[r].length
• 1 <= n <= 5 * 104
• 1 <= grid[r][c] <= 105

View Problem View Solution

Problem Statement

Có hai robot cùng xuất phát từ điểm (0,0) và muốn đến đích (1,n-1). Robot 1 di chuyển trước, sau đó Robot 2 di chuyển. Mọi ô mà Robot 1 đi qua sẽ bị set về 0. Nhiệm vụ của chúng ta là tính số điểm tối đa mà Robot 2 có thể thu được, với giả sử cả hai robot đều chơi tối ưu.

First Thoughts & Intuition

Xin chào các coder! Mình là Loser1 từ Learning AI with Loser. Bài toán hôm nay khá thú vị – một cuộc đua chiến thuật giữa hai robot! 🤖

Khi mới nhìn vào bài này, mình cảm thấy như đang chơi một game chiến thuật turn-based vậy! Mỗi robot là một player, và họ phải đưa ra quyết định tối ưu cho lượt đi của mình.

Hãy cùng phân tích chi tiết với một ví dụ nhỏ:

Ma trận ban đầu:
2  5  4
1  5  1

Phân tích lượt đi Robot 1:

Lựa chọn 1: Đi xuống ở cột 0         Lựa chọn 2: Đi xuống ở cột 1         Lựa chọn 3: Đi xuống ở cột 2
2  5  4                              2  5  4                              2  5  4
1  5  1                              1  5  1                              1  5  1

↓                                       ↓                                     ↓  

0  5  4                              0  0  4                              0  0  0
0  5  1                              0  0  1                              0  0  0

Sau mỗi lựa chọn của Robot 1, Robot 2 sẽ có các lựa chọn:

Case 1: Robot 1 đi xuống ở cột 0
0  5  4   → Robot 2 có thể lấy được max(5+4=9 bên trên, 0 bên dưới) = 9 điểm
0  5  1

Case 2: Robot 1 đi xuống ở cột 1
0  0  4   → Robot 2 có thể lấy được max(4 bên trên, 1 bên dưới) = 4 điểm
0  0  1

Case 3: Robot 1 đi xuống ở cột 2
0  0  0   → Robot 2 có thể lấy được max(0 bên trên, 5+1=6 bên dưới) = 6 điểm
0  0  0

Key Insights! 💡

1. Điểm cắt quan trọng:

• Robot 1 phải chọn một cột để đi xuống
• Cột này sẽ “cắt” ma trận thành 2 vùng:
  • Vùng trên-phải: Các ô còn lại trên hàng trên
  • Vùng dưới-trái: Các ô còn lại trên hàng dưới

1. Chiến lược tối ưu:

   Robot 1: "Mình phải chọn cột nào để Robot 2 lấy được ít điểm nhất"
   Robot 2: "Với mỗi cách cắt, mình sẽ chọn vùng có nhiều điểm hơn"

3. Visualize thông minh:

            [Cột j]
   2  5  4    ↓  
   1  5  1    

   Điểm Robot 2 = max(điểm_phải, điểm_trái)
   - điểm_phải = tổng các số bên phải trên hàng trên
   - điểm_trái = tổng các số bên trái trên hàng dưới

4. Prefix Sum Magic:

• Để tính nhanh tổng của một đoạn
• Hàng trên: Tính từ phải qua
• Hàng dưới: Tính từ trái qua

Từ những observation này, ta có thể thấy bài toán trở nên rõ ràng hơn:

• Robot 1 sẽ thử tất cả các cột có thể
• Với mỗi cột, tính điểm tối đa Robot 2 có thể lấy được
• Chọn cột cho kết quả nhỏ nhất

Ready to code? Let’s dive into the implementation! 🚀

Approach

1. Tính tổng cộng dồn:

• Upper sum: Tổng từ phải sang trái hàng trên
• Lower sum: Tổng từ trái sang phải hàng dưới

1. Với mỗi cột j:

• Tính điểm Robot 2 có thể lấy được nếu Robot 1 đi xuống ở cột j:
  Max(điểm phần trên bên phải, điểm phần dưới bên trái)

1. Kết quả:

• Lấy min của tất cả các trường hợp trên
  (vì Robot 1 muốn minimize điểm của Robot 2)

Code Implementation

class Solution {
public:
    long long gridGame(vector<vector<int>>& grid) {
        int n = grid[0].size();

        // Tính prefix sums
        vector<long long> upperSum(n, 0), lowerSum(n, 0);

        // Tính tổng hàng trên từ phải sang
        upperSum[n-1] = grid[0][n-1];
        for(int j = n-2; j >= 0; j--) {
            upperSum[j] = upperSum[j+1] + grid[0][j];
        }

        // Tính tổng hàng dưới từ trái sang
        lowerSum[0] = grid[1][0];
        for(int j = 1; j < n; j++) {
            lowerSum[j] = lowerSum[j-1] + grid[1][j];
        }

        // Tìm điểm tối thiểu mà Robot 2 có thể lấy được
        long long minPoints = LLONG_MAX;
        for(int j = 0; j < n; j++) {
            long long pointsRobot2 = max(
                j+1 < n ? upperSum[j+1] : 0,    // Điểm phần trên bên phải
                j > 0 ? lowerSum[j-1] : 0       // Điểm phần dưới bên trái
            );
            minPoints = min(minPoints, pointsRobot2);
        }

        return minPoints;
    }
};

Complexity Analysis

• Time: O(n) – duyệt mỗi cột một lần
• Space: O(n) – lưu prefix sums

Example Walkthrough

Cùng phân tích chi tiết từng bước giải bài toán này nhé! 🎮

Input Data:

grid = [[2, 5, 4],
        [1, 5, 1]]

Matrix Layout:

2  5  4
1  5  1

Step 1: Tính Prefix Sums

Để tối ưu việc tính tổng các đoạn, ta sẽ tính prefix sum cho cả 2 hàng:

Hàng trên (tính từ phải qua):

upperSum = [11, 9, 4]

Cách tính:
- upperSum[2] = 4
- upperSum[1] = 4 + 5 = 9
- upperSum[0] = 9 + 2 = 11

Hàng dưới (tính từ trái qua):

lowerSum = [1, 6, 7]

Cách tính:
- lowerSum[0] = 1
- lowerSum[1] = 1 + 5 = 6
- lowerSum[2] = 6 + 1 = 7

Step 2: Mô phỏng từng điểm cắt

Minh họa chi tiết:

Cắt tại cột 0:        Cắt tại cột 1:        Cắt tại cột 2:
0  5  4               0  0  4               0  0  0
0  5  1               0  0  1               0  0  0
Max(9, 0) = 9         Max(4, 1) = 4         Max(0, 6) = 6

Step 3: Tìm minimum của các maximum

Min(9, 4, 6) = 4

Answer: 4

Robot 1 nên chọn cắt tại cột 1, khi đó:

• Robot 2 chỉ có thể lấy tối đa 4 điểm
• Đây là kết quả tối ưu nhất có thể!

Visualization của đường đi tối ưu:

Robot 1 (đỏ):         Robot 2 (xanh):
2→5↓4                 2→5→4
1  5  1               1  5  1

Kết quả: Robot 2 được 4 điểm (đi theo đường xanh)

Qua ví dụ này, ta có thể thấy rõ chiến lược của cả hai robot:

• Robot 1: Chọn điểm cắt để minimize điểm của Robot 2
• Robot 2: Chọn đường đi để maximize điểm có thể lấy được

Note: Đây là một ví dụ điển hình của bài toán Min-Max trong Game Theory! 🎯

Key Insights

1. Prefix Sum Magic: Giúp tính tổng nhanh chóng O(1)
2. Min-Max Strategy: Robot 1 minimize, Robot 2 maximize
3. Cut Point Concept: Mỗi điểm cắt tạo ra 2 lựa chọn cho Robot 2

Tips & Tricks

1. Vẽ hình để hình dung rõ đường đi của robot
2. Test với case ma trận 2×2 trước khi thử các case phức tạp
3. Cẩn thận với overflow → dùng long long!

Chúc mọi người code vui! Hẹn gặp lại trong các bài Leetcode tiếp theo! 🚀

P/S: Follow mình tại Learning AI with Loser để cập nhật các bài giải Leetcode hàng ngày nhé! 💻✨

CODE EDITOR

#leetcode #leetcodedaily #algorithms #programming #learningwithlosers