Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Xin chào các bạn! Mình là Loser1 từ Learning AI with Loser. Hôm nay chúng ta sẽ cùng nhau khám phá một bài toán cực kỳ thú vị về sắp xếp mảng. Bài này ban đầu nhìn có vẻ phức tạp, nhưng khi hiểu được ý tưởng cốt lõi, các bạn sẽ thấy nó thật sự rất logic và thú vị! Let’s dive in! 🚀
Chào các bạn, bạn có thể xem Đề bài và Giải pháp của mình trên LeetCode tại đây:
- Đề bài: Xem tại đây
- Giải pháp: Xem tại đây
2948. Tạo Mảng Nhỏ Nhất Theo Thứ Tự Từ Điển Bằng Cách Hoán Đổi Phần Tử
MediumBạn được cung cấp một mảng số nguyên dương nums được đánh chỉ số từ 0 và một số nguyên dương limit.
Trong một thao tác, bạn có thể chọn hai chỉ số bất kỳ i và j và hoán đổi nums[i] và nums[j] nếu |nums[i] - nums[j]| <= limit.
Trả về mảng nhỏ nhất theo thứ tự từ điển có thể thu được bằng cách thực hiện thao tác trên bất kỳ số lần nào.
Mảng a được coi là nhỏ hơn mảng b theo thứ tự từ điển nếu tại vị trí đầu tiên mà a và b khác nhau, phần tử của a nhỏ hơn phần tử tương ứng của b. Ví dụ, mảng [2,10,3] nhỏ hơn mảng [10,2,3] vì chúng khác nhau tại chỉ số 0 và 2 < 10.
Example 1:
Input: nums = [1,5,3,9,8], limit = 2 Output: [1,3,5,8,9] Explanation: Áp dụng thao tác 2 lần: - Hoán đổi nums[1] với nums[2]. Mảng trở thành [1,3,5,9,8] - Hoán đổi nums[3] với nums[4]. Mảng trở thành [1,3,5,8,9] Chúng ta không thể thu được mảng nhỏ hơn theo thứ tự từ điển bằng cách thực hiện thêm thao tác nào nữa. Lưu ý rằng có thể thu được cùng kết quả bằng cách thực hiện các thao tác khác.
Example 2:
Input: nums = [1,7,6,18,2,1], limit = 3 Output: [1,6,7,18,1,2] Explanation: Áp dụng thao tác 3 lần: - Hoán đổi nums[1] với nums[2]. Mảng trở thành [1,6,7,18,2,1] - Hoán đổi nums[0] với nums[4]. Mảng trở thành [2,6,7,18,1,1] - Hoán đổi nums[0] với nums[5]. Mảng trở thành [1,6,7,18,1,2] Chúng ta không thể thu được mảng nhỏ hơn theo thứ tự từ điển bằng cách thực hiện thêm thao tác nào nữa.
Example 3:
Input: nums = [1,7,28,19,10], limit = 3 Output: [1,7,28,19,10] Explanation: [1,7,28,19,10] là mảng nhỏ nhất theo thứ tự từ điển mà chúng ta có thể thu được vì không thể áp dụng thao tác trên bất kỳ hai chỉ số nào.
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= 1091 <= limit <= 109
First Thoughts & Intuition 🎯
Khi mới nhìn vào bài này, mình liên tưởng đến một trò chơi xếp bi quen thuộc thời thơ ấu. Tưởng tượng chúng ta có một dãy bi với các màu sắc khác nhau:
Ban đầu:
[1] [5] [3] [9] [8]
🔴 🔵 🟢 🟡 ⚪
Rule: Chỉ được đổi chỗ 2 viên bi có số chênh lệch ≤ limitPhân tích sâu hơn về cách các số có thể "kết nối" 🔗
1. Khái niệm "Connected Components":
Với limit = 2:
[1] [5] [3] [9] [8]
╔═══════╗
║1 ↔ 3 ↔║5 Nhóm 1
╚═══════╝
9 ↔ 8 Nhóm 2
Giải thích:
- 1 và 3 có thể swap (|3-1| = 2)
- 3 và 5 có thể swap (|5-3| = 2)
- 9 và 8 có thể swap (|9-8| = 1)2. Visualization của quá trình Swap:
Step 1: Step 2: Step 3:
1 5 3 9 8 1 3 5 9 8 1 3 5 8 9
↕ ↕ ↕
1 3 5 9 8 1 3 5 8 9 Hoàn thành!3. Mental Model của Groups:
Original Array: [1, 5, 3, 9, 8]
Group Analysis:
Group 1: {1,3,5}
├── Có thể swap với nhau
├── Sorted: [1,3,5]
└── Original positions: [0,2,1]
Group 2: {8,9}
├── Có thể swap với nhau
├── Sorted: [8,9]
└── Original positions: [4,3]Detailed Approach 🛠️
1. Preprocessing: Tạo Pairs
// Original: [1,5,3,9,8]
// Tạo pairs (value, index):
[(1,0), (5,1), (3,2), (9,3), (8,4)]
// Mục đích:
// - Giữ track vị trí gốc
// - Dễ dàng sort và group2. Sort và Create Groups
// Sort pairs theo value:
[(1,0), (3,2), (5,1), (8,4), (9,3)]
// Group by limit:
if(current.value - prev.value <= limit) {
→ Same group
} else {
→ New group
}
// Result:
Group 1: [(1,0), (3,2), (5,1)]
Group 2: [(8,4), (9,3)]3. Process Each Group
Với mỗi nhóm:
1. Trích xuất các vị trí và giá trị
2. Sắp xếp các vị trí
3. Gán các giá trị đã sắp xếp vào các vị trí đã sắp xếp
Example Group 1:
Original: [(1,0), (3,2), (5,1)]
Positions: [0,2,1] → sort → [0,1,2]
Values: [1,3,5]
→ result[0]=1, result[1]=3, result[2]=5Super Detailed Code Implementation 💻
C++
class Solution {
public:
vector<int> lexicographicallySmallestArray(vector<int>& nums, int limit) {
int n = nums.size();
vector<pair<int,int>> pairs;
// Step 1: Tạo cặp (value, index)
for(int i = 0; i < n; i++) {
pairs.push_back({nums[i], i});
}
sort(pairs.begin(), pairs.end());
// Step 2: Tạo groups
vector<vector<pair<int,int>>> groups;
for(int i = 0; i < n; i++) {
if(i == 0 || pairs[i].first - pairs[i-1].first > limit) {
groups.push_back({pairs[i]});
} else {
groups.back().push_back(pairs[i]);
}
}
// Step 3: Fill result
vector<int> result(n);
for(auto& group : groups) {
vector<int> positions, values;
for(auto& p : group) {
positions.push_back(p.second);
values.push_back(p.first);
}
sort(positions.begin(), positions.end());
for(int i = 0; i < positions.size(); i++) {
result[positions[i]] = values[i];
}
}
return result;
}
};Complexity Analysis 📊
- Time Complexity:
O(nlogn) for sorting
├── Sort initial pairs: O(nlogn)
├── Process groups: O(n)
└── Sort positions in groups: O(klogk) where k < n- Space Complexity:
O(n) total
├── pairs vector: O(n)
├── groups vector: O(n)
└── result vector: O(n)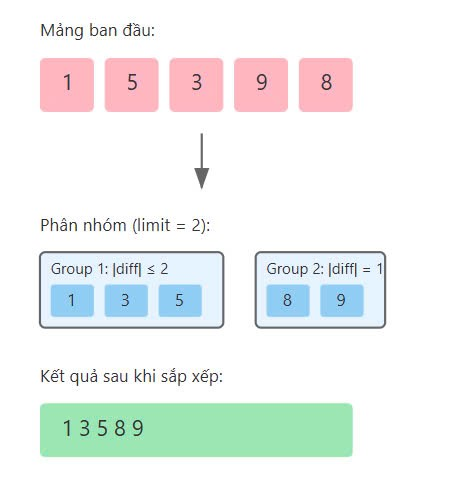Example Visualization 🎨
Hãy cùng xem một ví dụ hoàn chỉnh:
Input: nums = [1,5,3,9,8], limit = 2
Step-by-Step Visualization:
1️⃣ Initial State:
[1] [5] [3] [9] [8]
0 1 2 3 4 (indices)
2️⃣ Create & Sort Pairs:
[(1,0), (3,2), (5,1), (8,4), (9,3)]
↑ ↑ ↑ ↑ ↑
value,index pairs sorted by value
3️⃣ Group Formation:
Group 1: {(1,0), (3,2), (5,1)}
↑ ↑ ↑
|1-3|≤2 |3-5|≤2
Group 2: {(8,4), (9,3)}
↑ ↑
|8-9|≤2
4️⃣ Process Groups:
Group 1:
- Indices: [0,2,1] → [0,1,2]
- Values: [1,3,5]
Result: [1,3,5,_,_]
Group 2:
- Indices: [4,3] → [3,4]
- Values: [8,9]
Final: [1,3,5,8,9]Tips & Insights 💡
- Group Formation:
- Luôn sort trước khi tạo group
- Check difference giữa các phần tử liền kề
- Position Management:
- Giữ track vị trí gốc là crucial
- Sort positions trong mỗi group để optimize
- Edge Cases:
- Arrays với 1 phần tử
- Tất cả phần tử có thể swap
- Không có phần tử nào có thể swap
Chúc mọi người code vui! Hẹn gặp lại trong các bài Leetcode tiếp theo! 🚀
P/S: Follow mình tại Learning AI with Loser để cập nhật các bài giải Leetcode hàng ngày nhé! 💻✨
CODE EDITOR
#leetcode #leetcodedaily #algorithms #programming #learningwithlosers
