Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124

Xin chào các bạn yêu quý của Loser1! Hôm nay chúng ta sẽ tham gia một bữa tiệc đặc biệt – nơi mà việc sắp xếp chỗ ngồi trở thành một bài toán graph cực kỳ thú vị! Cùng khám phá nhé! 🎊
Công ty đang tổ chức một cuộc họp và có danh sách n nhân viên, chờ được mời tham dự. Họ đã sắp xếp một bàn tròn lớn, có thể chứa bất kỳ số lượng nhân viên nào.
Các nhân viên được đánh số từ 0 đến n – 1. Mỗi nhân viên có một người yêu thích và họ sẽ tham dự cuộc họp chỉ nếu họ có thể ngồi cạnh người yêu thích của mình tại bàn. Người yêu thích của một nhân viên không phải là chính họ.
Cho một mảng số nguyên chỉ mục 0 favorite, trong đó favorite[i] chỉ ra người yêu thích của nhân viên thứ i, trả về số lượng nhân viên tối đa có thể được mời tham dự cuộc họp.
Example 1:
Input: favorite = [2,2,1,2] Output: 3 Explanation: Hình ảnh trên cho thấy công ty có thể mời nhân viên 0, 1, và 2, và sắp xếp họ ngồi ở bàn tròn. Không thể mời tất cả nhân viên vì nhân viên 2 không thể ngồi cạnh nhân viên 0, 1, và 3 đồng thời. Lưu ý rằng công ty cũng có thể mời nhân viên 1, 2, và 3, và sắp xếp chỗ ngồi theo yêu cầu của họ. Số lượng nhân viên tối đa có thể được mời là 3.
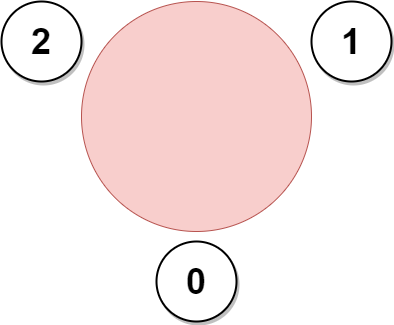
Example 2:
Input: favorite = [1,2,0] Output: 3 Explanation: Mỗi nhân viên đều có ít nhất một người yêu thích là người khác, và cách duy nhất công ty có thể mời họ là mời tất cả các nhân viên. Cách sắp xếp chỗ ngồi sẽ giống như trong hình ảnh ở ví dụ 1: - Nhân viên 0 ngồi giữa nhân viên 2 và 1. - Nhân viên 1 ngồi giữa nhân viên 0 và 2. - Nhân viên 2 ngồi giữa nhân viên 1 và 0. Số lượng nhân viên tối đa có thể được mời là 3.
Example 3:
Input: favorite = [3,0,1,4,1] Output: 4 Explanation: Hình ảnh trên cho thấy công ty sẽ mời nhân viên 0, 1, 3, và 4, và sắp xếp họ ngồi ở bàn tròn. Nhân viên 2 không thể được mời vì hai chỗ cạnh người yêu thích của họ là nhân viên 1 đã được chiếm. Vì vậy, công ty sẽ không mời họ tham dự cuộc họp. Số lượng nhân viên tối đa có thể được mời là 4.
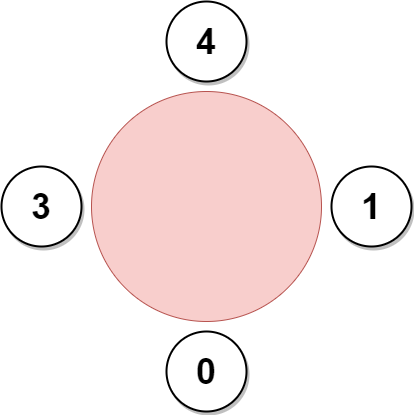
Constraints:
n == favorite.length2 <= n <= 10^50 <= favorite[i] <= n - 1favorite[i] != iKhi mới nhìn vào bài này, mình liên tưởng đến việc tổ chức một bữa tiệc công ty với rất nhiều mối quan hệ "crush" phức tạp:
Một bàn tiệc tròn:
👤
👤 👤 Mỗi người muốn ngồi cạnh
👤 👤 "crush" của mình!
👤 👤
👤Các mối quan hệ thường xuất hiện theo các pattern sau:
1. Tình Yêu Đơn Phương: 2. Tình Yêu Đôi Bên:
A → B → C A ↔ B
(Một chiều) (Hai chiều)
3. Chuỗi Tình Cảm: 4. Hội Fan Club:
A → B → C → D A ← B
(Chain) ↑ ↑
C DInput: [2,2,1,2]
Visualize mối quan hệ:
Employee 0: "Tôi chỉ muốn ngồi cạnh số 2!"
0 → 2
Employee 1: "Số 2 là idol của tôi!"
1 → 2
Employee 2: "Tôi thích số 1!"
2 → 1
Employee 3: "Số 2 là crush của tôi!"
3 → 2
Vẽ graph:
0
↓
3→2←1
↓
1Trước khi dive vào solution, hãy hiểu rõ các khái niệm quan trọng:
1. In-degree: Số lượng người thích một người
[2,2,1,2] → inDegree[2] = 3 (được 3 người thích)
2. Cycle: Vòng tròn tình cảm
A → B → C → A (Cycle length = 3)
3. Chain: Chuỗi tình cảm một chiều
A → B → C → D (Chain length = 3)Case 1: Cycle Length > 2
┌────────────┐
A → B → C → D│
└────────────┘
- Tất cả có thể ngồi cùng nhau!
- Count = cycle length
Case 2: Cycle Length = 2 + Chains
A ↔ B Count = 2 +
↑ ↑ (length of chains)
C D └── C: +1
↑ └── D: +1
EStep 1: Initialize Data Structures
class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
int n = favorite.size();
vector<int> inDegree(n, 0); // Số người thích mỗi người
vector<int> chainLengths(n, 0); // Độ dài chuỗi tới mỗi người
vector<bool> visited(n, false); // Đánh dấu đã xétStep 2: Calculate In-degrees
// Tính số người thích mỗi người
for(int fav : favorite) {
inDegree[fav]++;
}
// Visualize:
// favorite = [2,2,1,2]
// inDegree = [0,1,3,0]
// ↑ không ai thíchStep 3: BFS Process
queue<int> q;
// Bắt đầu từ những người không được ai thích
for(int i = 0; i < n; i++) {
if(inDegree[i] == 0) q.push(i);
}
while(!q.empty()) {
int person = q.front();
q.pop();
visited[person] = true;
// Cập nhật độ dài chuỗi
int nextPerson = favorite[person];
chainLengths[nextPerson] = chainLengths[person] + 1;
// Nếu đã xét hết người thích nextPerson
if(--inDegree[nextPerson] == 0) {
q.push(nextPerson);
}
}Step 4: Process Cycles
int maxCycle = 0; // Cho cycles > 2
int totalChains = 0; // Cho cycles = 2
for(int i = 0; i < n; i++) {
if(!visited[i]) {
int cycleLength = 0;
int curr = i;
// Tìm độ dài cycle
while(!visited[curr]) {
visited[curr] = true;
curr = favorite[curr];
cycleLength++;
}
if(cycleLength == 2) {
// Case đặc biệt: cycle 2 người
totalChains += 2 +
chainLengths[i] +
chainLengths[favorite[i]];
} else {
// Cycles thông thường
maxCycle = max(maxCycle, cycleLength);
}
}
}
return max(maxCycle, totalChains);
}
};Hãy phân tích từng bước với ví dụ: [3,0,1,4,1]
Vẽ graph:
2 → 1 ← 4
↓ ↑
0 → 3
Initial arrays:
Index: 0 1 2 3 4
favorite: [3, 0, 1, 4, 1]
inDegree: [1, 2, 0, 1, 1]1. Start từ node 2 (inDegree = 0):
- Visit 2 → 1
- chainLengths[1] = 1
2. Process neighbors:
- inDegree[1]-- = 1 (vẫn > 0)
3. Final chainLengths:
[1, 1, 0, 0, 0]Find cycles:
1. Start từ node 0:
0 → 3 → 4 → 1 → 0
(Cycle length = 4)
2. Process cycle:
maxCycle = max(maxCycle, 4) = 4max(maxCycle, totalChains)
= max(4, 0)
= 4 employees!
Seating arrangement:
0 → 3 → 4 → 1
└───────────┘ Vẽ graph trước khi code:
- Dùng arrows cho directed edges
- Circle các cycles
- Mark các chain lengths Case 1: [1,0]
- Simple 2-cycle
Case 2: [1,2,3,1]
- 3-person cycle
Case 3: [1,2,0,0,3]
- Multiple cycles - Sử dụng queue cho BFS
- Tránh tính toán lặp
- Kết thúc code khi có thểChúc mọi người code vui! Hẹn gặp lại trong các bài Leetcode tiếp theo! 🚀
P/S: Follow mình tại Learning AI with Loser để cập nhật các bài giải Leetcode hàng ngày nhé! 💻✨
CODE EDITOR
#leetcode #leetcodedaily #algorithms #programming #learningwithlosers