Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Xin chào các bạn yêu quý của Loser1! Ngày thứ hai của năm mới 2025, chúng ta sẽ cùng nhau khám phá một cách giải quyết bài Hard bằng Union-Find và BFS cực kỳ thú vị! Let’s learn together! 🚀
2493. Divide Nodes Into the Maximum Number of Groups
HardCho một số nguyên dương n đại diện cho số lượng nút trong một đồ thị vô hướng. Các nút được đánh số từ 1 đến n.
Bạn cũng được cho một mảng 2D edges, trong đó edges[i] = [ai, bi] cho biết có một cạnh hai chiều giữa các nút ai và bi. Lưu ý rằng đồ thị có thể không liên thông.
Chia các nút trong đồ thị thành m nhóm (chỉ số bắt đầu từ 1) sao cho:
- Mỗi nút trong đồ thị thuộc về đúng một nhóm.
- Với mỗi cặp nút trong đồ thị mà có một cạnh
[ai, bi], nếuaithuộc nhóm có chỉ sốx, vàbithuộc nhóm có chỉ sốy, thì|y - x| = 1.
Trả về số nhóm tối đa mà bạn có thể chia các nút. Nếu không thể chia theo yêu cầu, trả về -1.
Example 1:
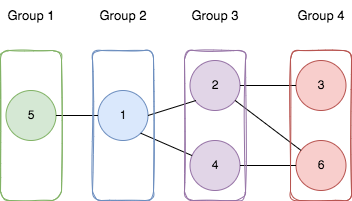
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]] Output: 4 Explanation: Như hình dưới đây, chúng ta: - Thêm nút 5 vào nhóm thứ nhất. - Thêm nút 1 vào nhóm thứ hai. - Thêm các nút 2 và 4 vào nhóm thứ ba. - Thêm các nút 3 và 6 vào nhóm thứ tư. Chúng ta có thể thấy rằng mỗi cạnh đều được thoả mãn. Nếu tạo nhóm thứ năm và di chuyển một nút từ nhóm ba hoặc bốn vào nó, ít nhất một cạnh sẽ không được thoả mãn.
Example 2:
Input: n = 3, edges = [[1,2],[2,3],[3,1]] Output: -1 Explanation: Nếu thêm nút 1 vào nhóm thứ nhất, nút 2 vào nhóm thứ hai và nút 3 vào nhóm thứ ba để thoả mãn hai cạnh đầu tiên, chúng ta sẽ thấy rằng cạnh thứ ba sẽ không được thoả mãn. Có thể chứng minh rằng không thể tạo nhóm hợp lệ.
Constraints:
1 <= n <= 5001 <= edges.length <= 104edges[i].length == 21 <= ai, bi <= nai != bi- Chỉ có một cạnh duy nhất giữa mỗi cặp đỉnh.
First Thoughts & Intuition 🧠
Khi nhìn vào bài này, mình thấy có hai ý tưởng chính:
1. Component Analysis 🔍
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Component visualization:
5 Nhận xét:
| - Nodes trong cùng component
1 - Phải đảm bảo không có chu trình lẻ
/ | \ - Cần tìm depth lớn nhất có thể
2 | 4 cho mỗi component
/| \_/
3 62. Level Assignment 📚
Level 1: [5] Chiến lược:
Level 2: [1] - Dùng BFS để gán level
Level 3: [2,4] - Check chu trình lẻ
Level 4: [3,6] - Lưu max depth cho mỗi componentDetailed Approach 🎯
1. Disjoint Set Implementation 🌟
C++
class DisjointSet {
public:
unordered_map<int, int> leader; // Track root của mỗi node
// Tìm root của node với path compression
int findRoot(int node) {
if (!leader.count(node)) // Node chưa có trong map
leader[node] = node; // Khởi tạo là chính nó
if (leader[node] != node) // Nếu không phải root
leader[node] = findRoot(leader[node]); // Compress path
return leader[node];
}
// Unite hai node a và b
void unite(int a, int b) {
leader[findRoot(b)] = findRoot(a);
}
};2. Main Solution Flow 🚀
C++
int magnificentSets(int n, vector<vector<int>>& edges) {
// Step 1: Khởi tạo DSU và adjacency list
auto dsu = DisjointSet();
vector<vector<int>> adjacencyList(n + 1);
// Step 2: Build graph và unite components
for(auto& edge : edges) {
adjacencyList[edge[0]].push_back(edge[1]);
adjacencyList[edge[1]].push_back(edge[0]);
dsu.unite(edge[0], edge[1]); // Unite trong cùng component
}
// Step 3: BFS từ mỗi node để tìm max depth
vector<int> groupDepth(n + 1, 0);
for(int start = 1; start <= n; start++) {
// Initialize BFS
deque<pair<int, int>> q = {{start, 1}};
vector<int> levels(n + 1, 0);
levels[start] = 1;
// Process BFS
while(!q.empty()) {
auto [node, depth] = q.front();
q.pop_front();
// Check và process neighbors
for(auto& neighbor : adjacencyList[node]) {
if(!levels[neighbor]) {
q.push_back({neighbor, depth + 1});
levels[neighbor] = depth + 1;
}
// Check odd cycle
if(depth == levels[neighbor])
return -1; // Có chu trình lẻ
}
// Update max depth cho component
int root = dsu.findRoot(start);
groupDepth[root] = max(groupDepth[root], depth);
}
}
// Step 4: Tính tổng depth của tất cả components
return accumulate(groupDepth.begin(), groupDepth.end(), 0);
}Example Walkthrough 🎮
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Step 1: Build Graph & Unite
DSU state:
1 ← 2 ← 3
↑ ↑
4 6
↑
5
Step 2: BFS từ node 5
Iteration 1:
Queue: (5,1)
Levels: [5:1]
Iteration 2:
Queue: (1,2)
Levels: [5:1, 1:2]
Iteration 3:
Queue: (2,3), (4,3)
Levels: [5:1, 1:2, 2:3, 4:3]
Iteration 4:
Queue: (3,4), (6,4)
Levels: [5:1, 1:2, 2:3, 4:3, 3:4, 6:4]
Final groupDepth[root_1] = 4Complexity Analysis 📊
Time Complexity: O(N * (N + E))
├── DSU operations: O(α(N)) ≈ O(1)
├── BFS từ mỗi node: O(N * (N + E))
└── Total: O(N * (N + E))
Space Complexity: O(N + E)
├── Adjacency List: O(E)
├── DSU: O(N)
├── BFS Queue: O(N)
└── Levels Array: O(N)Tips & Tricks 💡
- Union-Find Optimization:
- Sử dụng path compression trong `findRoot`
- Lưu trữ leader trong `unordered_map`
- Kết hợp (unite) theo root node- BFS Implementation:
- Sử dụng `deque` để tối ưu hóa các thao tác
- Theo dõi `levels` để phát hiện chu trình
- Cập nhật `max depth` cho mỗi component- Edge Cases:
Single Node: Odd Cycle: Multiple Components:
1 1---2 1 4
\ / | |
3 2---3 5Chúc mừng năm mới 2025! Hy vọng bài Hard này sẽ giúp các bạn hiểu sâu hơn về Union-Find và BFS! 🎊
P/S: Follow mình tại Learning AI with Loser để cập nhật các bài giải Leetcode hàng ngày nhé! 💻✨
CODE EDITOR
#leetcode #leetcodedaily #algorithms #programming #learningwithlosers #newyear2025t bài toán.
